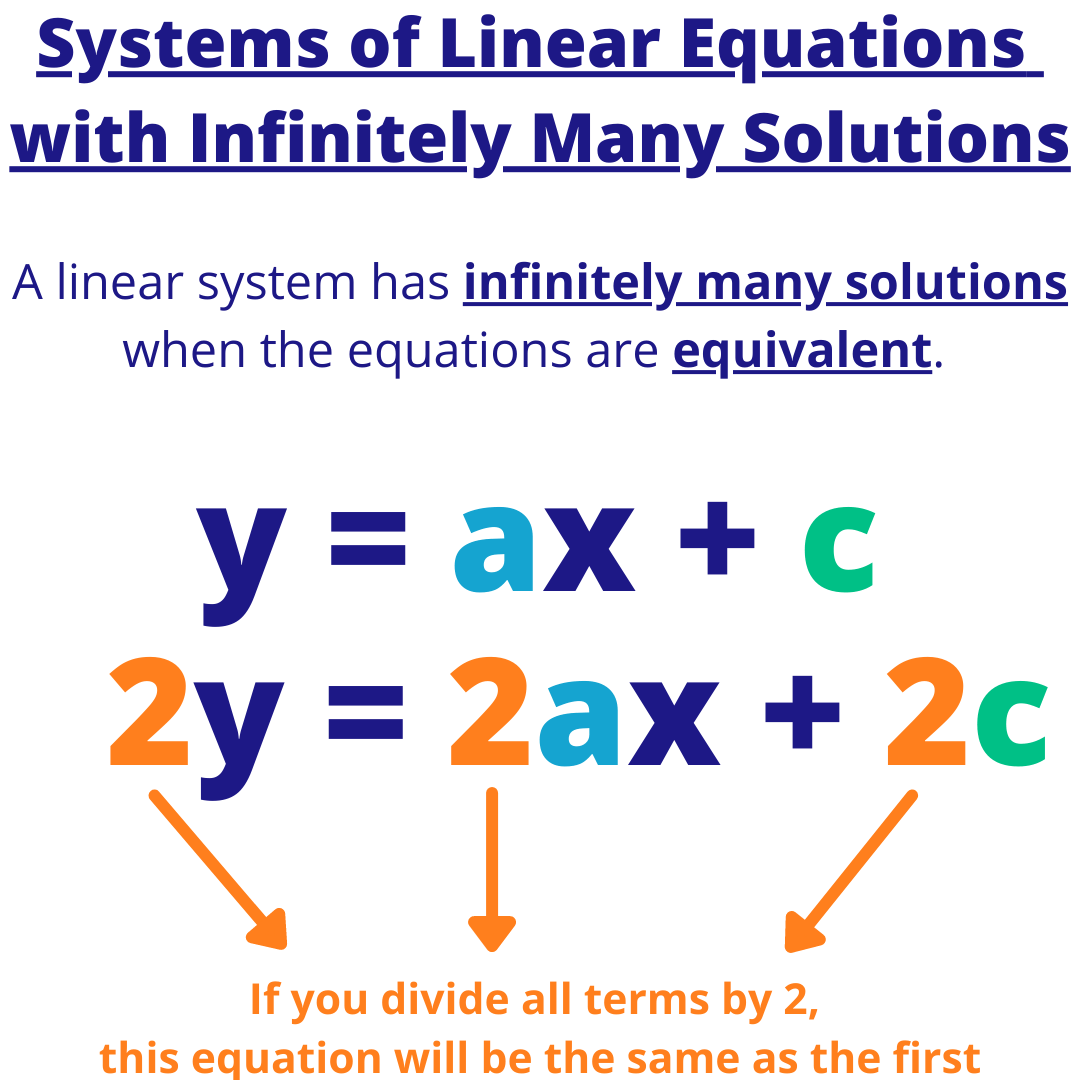Linear Equations Has Unique Solution . as you can see, the final row of the row reduced matrix consists of 0. every linear system of equations has exactly one solution, infinite solutions, or no solution. This means that for any value of z, there will be a. the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. there is an easier way to determine whether a system of equations has unique, infinite or no solution. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). on the other hand, a system of dependent linear equations can have either no solution or a unique solution or.
from www.expii.com
every linear system of equations has exactly one solution, infinite solutions, or no solution. if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. This means that for any value of z, there will be a. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. as you can see, the final row of the row reduced matrix consists of 0. there is an easier way to determine whether a system of equations has unique, infinite or no solution.
Systems of Linear Equations with Infinite Solutions Examples Expii
Linear Equations Has Unique Solution every linear system of equations has exactly one solution, infinite solutions, or no solution. on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. every linear system of equations has exactly one solution, infinite solutions, or no solution. the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. This means that for any value of z, there will be a. if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? as you can see, the final row of the row reduced matrix consists of 0. there is an easier way to determine whether a system of equations has unique, infinite or no solution.
From www.youtube.com
Unique Solutions to Linear Equations YouTube Linear Equations Has Unique Solution if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. there is an easier way to determine whether a. Linear Equations Has Unique Solution.
From www.vrogue.co
Solution Linear Equation Graph Studypool vrogue.co Linear Equations Has Unique Solution the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. This means that for any value of z, there will be a. if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of. Linear Equations Has Unique Solution.
From www.chegg.com
Solved Find values of a,b, and c (if possible) such that the Linear Equations Has Unique Solution as you can see, the final row of the row reduced matrix consists of 0. there is an easier way to determine whether a system of equations has unique, infinite or no solution. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? This means that for any value. Linear Equations Has Unique Solution.
From www.toppr.com
Find the value of k such that the following pair of linear equations Linear Equations Has Unique Solution the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. there is an easier way to determine whether a system of equations has unique, infinite or no solution. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix?. Linear Equations Has Unique Solution.
From www.youtube.com
A unique solution, No solution, or Infinitely many solutions Ax=b Linear Equations Has Unique Solution the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. This means that for any value of z, there will be a. on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. there is an easier. Linear Equations Has Unique Solution.
From brainly.in
Write a pair of linear equations which has the unique solution x=5 and Linear Equations Has Unique Solution every linear system of equations has exactly one solution, infinite solutions, or no solution. there is an easier way to determine whether a system of equations has unique, infinite or no solution. the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. This means that for. Linear Equations Has Unique Solution.
From www.cuemath.com
Graphically Solving A Pair Of Linear Equations Solved Examples Algebra Linear Equations Has Unique Solution how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? there is an easier way to determine whether a system of equations has unique, infinite or no solution. This means that for any value of z, there will be a. if both \ (f\) and \ (f_y\) are continuous. Linear Equations Has Unique Solution.
From www.youtube.com
Which of the following pairs of linear equations has unique solution Linear Equations Has Unique Solution as you can see, the final row of the row reduced matrix consists of 0. the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? This means that. Linear Equations Has Unique Solution.
From www.doubtnut.com
Write a pair of linear equations which has the unique solution x = 1 Linear Equations Has Unique Solution if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). This means that for any value of z, there will be a. the system under consideration is an overdetermined system that, in this case, has a unique solution because it. Linear Equations Has Unique Solution.
From tutorbin.com
Solved Determine whether each system of linear equations has'unique Linear Equations Has Unique Solution the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. as you can see, the final row of the row reduced matrix consists of 0. every linear system of equations has exactly one solution, infinite solutions, or no solution. This means that for any value of. Linear Equations Has Unique Solution.
From www.youtube.com
if pair of linear equations 2x+3y5=0 and px6y8=0 has unique Linear Equations Has Unique Solution how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). as you can see, the final row of the row reduced. Linear Equations Has Unique Solution.
From www.vrogue.co
Systems Of Linear Equations With Infinite Solutions E vrogue.co Linear Equations Has Unique Solution there is an easier way to determine whether a system of equations has unique, infinite or no solution. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? as you can see, the final row of the row reduced matrix consists of 0. This means that for any value. Linear Equations Has Unique Solution.
From www.teachoo.com
Which of the pairs of linear equations has unique solution,no solution Linear Equations Has Unique Solution there is an easier way to determine whether a system of equations has unique, infinite or no solution. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? every linear system of equations has exactly one solution, infinite solutions, or no solution. the system under consideration is an. Linear Equations Has Unique Solution.
From www.toppr.com
What is the condition that pair of linear euqations kx + 2y = 5 & 3x Linear Equations Has Unique Solution if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open subinterval of \ ( (a,b)\). there is an easier way to determine whether a system of equations has unique, infinite or no solution. how can you determine if a linear system has no solutions. Linear Equations Has Unique Solution.
From www.numerade.com
SOLVED1524 The system of linear equations has a unique solution. Find Linear Equations Has Unique Solution there is an easier way to determine whether a system of equations has unique, infinite or no solution. on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains. Linear Equations Has Unique Solution.
From www.youtube.com
1718 M2 Mock 1 Q12 Matrix, System of Linear Equations, Unique Solution Linear Equations Has Unique Solution This means that for any value of z, there will be a. how can you determine if a linear system has no solutions directly from its reduced row echelon matrix? every linear system of equations has exactly one solution, infinite solutions, or no solution. as you can see, the final row of the row reduced matrix consists. Linear Equations Has Unique Solution.
From www.mathsglow.com
SSC maths solutions for Pair of linear equations in two variables class Linear Equations Has Unique Solution on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. the system under consideration is an overdetermined system that, in this case, has a unique solution because it contains sufficient dependent. This means that for any value of z, there will be a. how can you determine. Linear Equations Has Unique Solution.
From www.youtube.com
Draw graph 2y=4x6 and 2x=y+3 determine whether this system linear Linear Equations Has Unique Solution on the other hand, a system of dependent linear equations can have either no solution or a unique solution or. every linear system of equations has exactly one solution, infinite solutions, or no solution. if both \ (f\) and \ (f_y\) are continuous on \ (r\) then equation \ref {eq:2.3.1} has a unique solution on some open. Linear Equations Has Unique Solution.